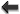A Appendix
A.1 Neutral landscape models
Ecology is increasingly using “virtual” landscape modelling to evaluate the links between ecological processes and the spatial and temporal patterns they produce. Neutral landscape models, in particular, were designed to generate a landscape in the absence of a studied ecological process (Gardner et al., 1987; Saura and Martínez-Millán, 2000*). Unlike explicit LM that would simulate dynamic functions and relations between landscape elements, neutral models do not intend to produce the spatial pattern of any particular observed landscape. Neutral models deal more precisely with one or several characteristics of composition and configuration of real landscapes (Gaucherel et al., 2006a; With and King, 1997*). These models may belong to most of the above-mentioned landscape types (agricultural, forested, arid or urban mosaics). After comparisons with observed landscapes, spatial landscapes and structures simulated by neutral models can discriminate between influences likely to be caused by random (i.e., neutral) rather than real structures. Their contribution to landscape ecology has been extensive: development of spatial indices to describe landscape configurations, forecasting of configurations essential for ecological phenomena, definition of connectivity, understanding of landscape influence on animal species or seeds, development of a generic model of spatial complexity, identification of ecological consequences of spatial homogeneity. Many ecological applications for neutral models are found in studies on the dispersion and abundance of animal populations, forest fires or biodiversity (With and King, 1997).
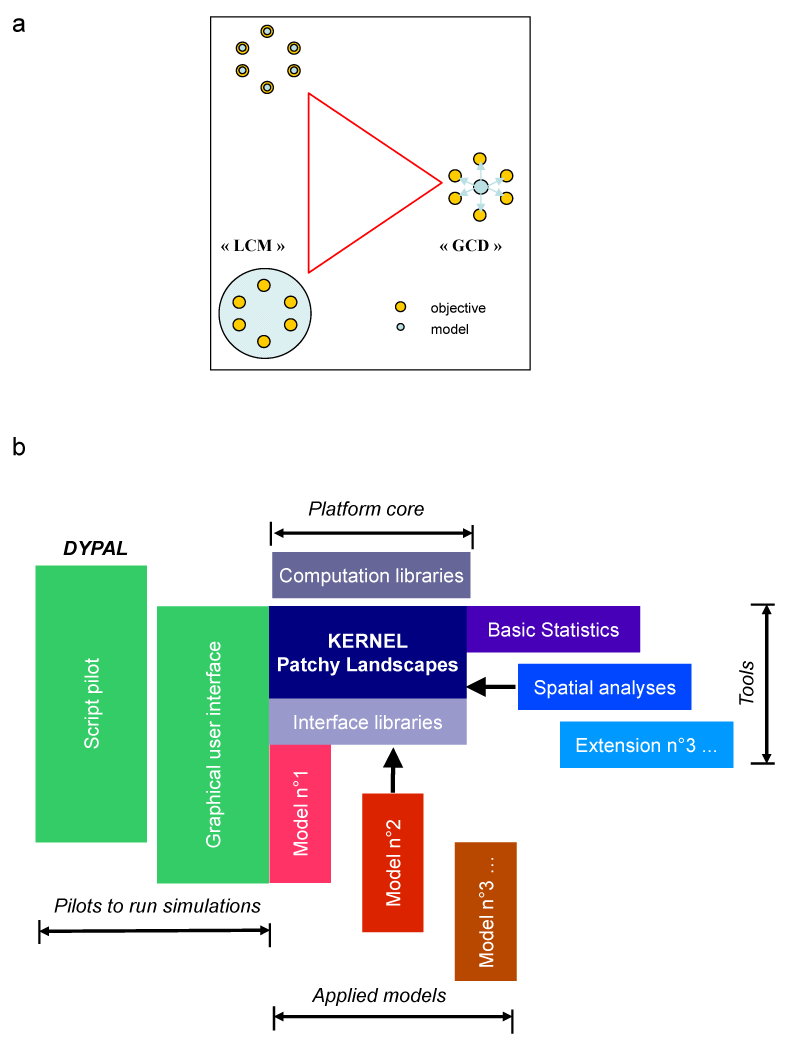
There is a gradation of virtual landscapes, from the pure neutral model up to the almost explicit model (Figure 2*). Landscapes simulated by neutral models are often pixel matrices (called raster mode) for which a land cover is associated to each pixel. In the simplest neutral model, random distributions of the two present classes are performed by associating each pixel with a probability of belonging to one of the classes. This simple model only constrains class densities (i.e., composition) and not their spatial distributions. The absence of spatial correlations in such models does not allow accounting for the complexity of real landscapes (Saura and Martínez-Millán, 2000*). Although rudimentary, the random model has identified characteristics such as the critical value of the class probability beyond which certain properties (e.g., connectivity) of a simulated landscape are drastically different. More sophisticated, some configuration models also define a directional adjacency matrix Q. The Qij elements translate the probability of a pixel belonging to type i being adjacent to a pixel of type j, with adjacency possibly defined according to direction and distance (Gardner, 1999). These models can be refined by the modified random cluster method, which controls the shapes of simulated classes, by aggregating pixels together (Saura and Martínez-Millán, 2000). Many other neutral LMs have been proposed, for example on the basis of an iterative process changing some pixel classes, and thus leading to hierarchical or fractal patterns (Figure 2*b).
All neutral models presented here deal with landscape considered as a continuous entity in raster mode, where the pixel is an autonomous (yet not independent) entity. Several ecological studies, however, need to represent landscape with a patchy map in which areas are considered homogeneous from the point of view of the ecological process studied (Kotliar and Wiens, 1990; Levin et al., 1993). This becomes crucial in anthropogenic landscapes and those marked with linear networks (roads, rivers, hedgerows, etc.) or field limits. For this purpose, new neutral LMs have been developed (Gaucherel, 2008), which sometimes use a Gibbs algorithm to select patch classes or to draw linear networks. Furthermore, neutral LMs appear increasingly relevant as a basis to build a coherent theoretical framework for dynamical landscapes. By offering a null-hypothesis test, they help to discriminate between ecological processes and random functions. By handling more or less simple statistical equations to describe landscapes, they offer opportunities to capture patterns and/or dynamics within parsimonious and coherent formalisms.
A.2 Landscape self-organization
The concept of self-organization, inspired from the complexity theory and from physical systems, offers an appealing way for landscape modelling. By definition, a landscape would be called self-organized if at least one of its properties (e.g., the spatial distribution of tree densities) exhibits regular (i.e., with non random patterns at a specific scale) or self-similar (i.e., fractal, with a power-law scaling) behaviours (Rietkerk and Van de Koppel, 2008*; Solé and Bascompte, 2006*). The scientific community questions whether landscapes are often self-organized. If not, why? If yes, which ecological processes are responsible for the landscape self-organization?
The concept of self-organization has often been advocated to investigate ecological processes. For example, it has been observed that forested landscapes, both in temperate and tropical areas, sometimes exhibit self-organized patterns (Gaucherel, 2011*; Scanlon et al., 2007; Solé et al., 1999). However, because it is still a phenomenological approach, self-organization is of little help to understand the forest functioning, and only provides a starting reference framework. By focusing on heterogeneous landscape dynamics, we wish to understand by which mechanisms (vegetation dispersion, competition, land-cover allocation…) self-organized structures emerge (Rietkerk and Van de Koppel, 2008; Solé and Bascompte, 2006). It is equally important to understand when self-organization fails to explain observed landscapes. What are the respective roles and weights of local rules (bottom-up controls), of more global rules (top-down controls), and of scaling properties in driving the fate of landscapes? What are the respective roles of human decisions and natural forcings? Under which conditions are simplified (yet realistic) landscape systems self-organized?
Two of the most common theoretical forest models exhibit self-organization and present interesting opportunities to understand complex landscapes: optimized and Turing-like patterns. On the one hand, recent studies have presented newly scaling properties for forested landscapes. Highlighting a link with optimal control theory and physical statistics, it is advocated that extended patchy forests may sometimes self-organize by optimizing the ecological processes involved in their generation. Preliminary forest models, based on a Hamiltonian or other summarizing functions of the forest element interactions have been developed in order to test the landscape self-organization hypothesis (Gaucherel, 2011; Lefever and Lejeune, 1997*). On the other hand, Turing-like patterns concern periodical vegetation covers generated on the basis of opposite forces acting at different scales (Couteron and Lejeune, 2001; Lejeune et al., 2002*). A reaction-diffusion process or, analogously, a competition-facilitation process has already proven its ability to reproduce the properties of a large range of spotted, gapped or banded vegetation covers (Lefever and Lejeune, 1997; Lejeune et al., 2002). Such vegetations appear to be self-organized too, yet on the basis of other patterns than the auto-similar properties mentioned earlier. By suggesting a relatively simple concept to describe landscapes, self-organization again offers opportunities to capture patterns and/or dynamics within parsimonious and coherent formalisms.
 |
 |
 |
Living Rev. Landscape Res., 8 (2014), 2, doi:10.12942/lrlr-2014-2, URL (accessed <date>): http://lrlr.landscapeonline.de/lrlr-2014-2.
This work is licensed under a Creative Commons License.
© The author(s), except where otherwise noted.